@ g Ivan Prisyazhnyy on software engineering

Transaction isolation anomalies

30 Jul 2019

This document contains simple examples and explanations of transaction isolation anomalies well known since the late ’90s. The work based on papers [1], [2], [3]. I hope it will be helpful for someone as a quick reference.

List of covered anomalies include:

Model

On database model and transactions, I encourage you to read [1]-[3].

In short:

  1. The database consists of objects: rows or tuples;
  2. Objects can be read or written by transactions;
  3. Transaction reads and writes objects in some specific order;
  4. An object has one or more versions.
  5. Transaction can read any version of an object.
  6. Transaction write generates a new version of an object.

Histories

Transaction execution form histories. There are good and bad histories that we don’t want to happen.

A history H over a set of transactions consists of two parts — a partial order of events E (e.g., read, write, abort, commit) of those transactions, and a version order, \(<<\), that is a total order on committed versions of each object.

Predicates

There are predicate reads and writes. A predicate is a boolean condition: Id = 1 or WHERE DEPT = SALES or WHERE Age > 18.

For example, list all employees from sales department:

SELECT * FROM EMPLOYEE WHERE DEPT = SALES;

A query based on a predicate \(P\) (i.e. DEPT = SALES) by transaction \(T_i\) is represented in a history as \(r_i(P: Vset(P)) \, r_i(x_j) \, r_i(y_k) ...\), where \(x_j\) , \(y_k\) are the object versions in \(Vset(P)\) that was read, \(Vset(P)\) is a set of selected versions of objects that matches \(P\) for this read, and \(T_i\) reads these versions.

Example of predicate-write, rise salary for sales:

UPDATE EMPLOYEE SAL = SAL + $10 WHERE DEPT=SALES;

In this document I will use simplified notation in which I only mention that the operation has predicate: \(r_i(P: Vset(P))\) without mentioning the versions actually read by it.

Serialization Graph

Direct serialization graph arising from a history H, denoted by \(DSG(H)\) is a graph in which each node corresponds to a committed transaction and directed edges correspond to different types of direct conflicts.

There is a read/write/anti-dependency edge from transaction \(T_i\) to transaction \(T_j\) if \(T_j\) directly read/write/anti-depends on \(T_i\).

Basic transactions conflicts

Read-dependency (wr)

Transaction \(T_j\) directly read-depends on transaction \(T_i\) if \(T_i\) installs some object version \(x_i\) and \(T_j\) reads \(x_i\).

The relation is called wr because one transaction writes an object and the dependant transaction reads it.

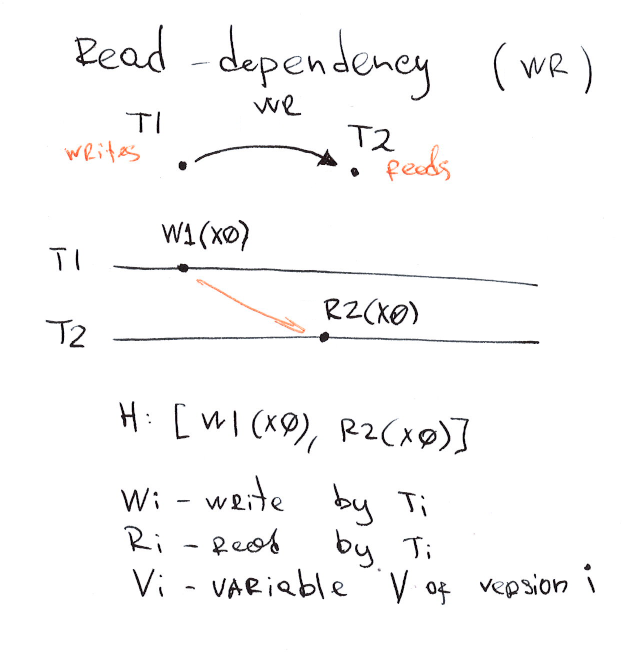
  • \(W_i\) denotes write operation by transaction \(T_i\);
  • \(R_i\) denotes read operation by transaction \(T_i\);
  • \(Xj, X[j], X(j)\) denotes an object \(X\) of version \(j\)

\(W_1(X_0)\) means transaction \(T_1\) wrote object \(X\) of version 0 in history \(H\).

In this example transaction \(T_2\) reads an object \(X\) written by the transaction \(T_1\) and thus item-read-depends on \(T_1\). This wr dependency is outlined as an orange arrow in the graph from \(T_1\) to \(T_2\) over \(x\): \(wr[x]\) or \(W_1(x_0) -wr[x]-> R_2(x_0)\).

update test set value = 1 where id = 1;  -- Ti: Wi(x0)
select * from test where id = 1;         -- Tj: Rj(x0)

Change the matches of predicate-based read (wr)

\(T_i\) changes the matches of a predicate-based read \(r_j (P: Vset(P))\) if \(T_i\) installs \(x_i\) , \(x_h\) immediately precedes \(x_i\) in the version order, and \(x_h\) matches \(P\) whereas \(x_i\) does not or vice-versa. In this case, we also say that \(x_i\) changes the matches of the predicate-based read.

This is another case of wr dependency when first transaction installs a new object version which then appears (or disappears) in the predicate-read results executed by the second transaction. And by doing so, it changes the predicate-read matching set \(Vset(P)\).

Transaction \(T_2\) sees \(x_0\) in the first read. In the second read it observes nothing due to \(x_0\) was just replaced with the \(x_1\) by the \(T1\) and \(x_1 \notin Vset(P)\) of \(r_2(P)\): \(W_1(x_1) -wr[x]-> R_2(P: Vset(P))\), \(r_21(Vset(P)=\{x_0\}), r_22(Vset(P)=\{\})\).

select * from test where value > 0;         -- Tj: Rj(P: Vset(P): x0)
update test set value = 0 where id = 1;     -- Ti: Wi(x1)
select * from test where value > 0;         -- Tj: Rj(P: Vset(P): {})

Write-dependency (ww)

A transaction \(T_j\) directly write-depends on \(T_i\) if \(T_i\) installs a version \(x_i\) and \(T_j\) installs x’s next version (after \(x_i\)) in the version order.

The relation is called ww because one transaction writes an object and the dependant transaction overwrites it. ww cycles arises phenomena known as dirty writes.

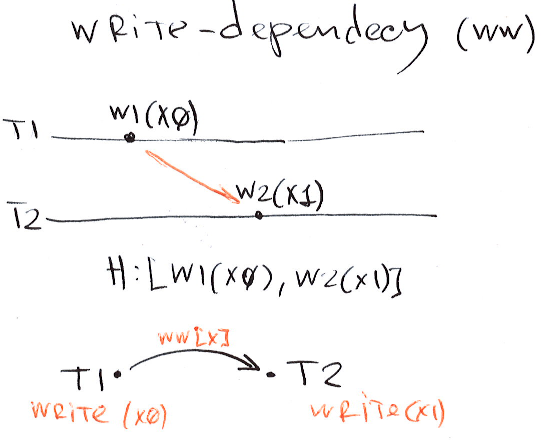
In this example transaction \(T_2\) overwrites an object \(x\) written by the transaction \(T_1\) and thus write-depends on \(T_1\). This ww dependency is outlined as an orange arrow in the graph from \(T_1\) to \(T_2\) over \(x\): \(W_1(X_0) -ww[x]-> W_2(X_1)\).

update test set value = 1 where id = 1;  -- Ti: Wi(x0)
update test set value = 2 where id = 1;  -- Tj: Wj(x1)

Anti-dependency (rw)

An anti-dependency occurs when a transaction overwrites a version observed by some other transaction. One transaction reads an object which is then updated by another transaction: read-write-depends (rw).

There is a small difference between the item-anti-dependency and predicate-anti-dependency but its not significant, even though they form different levels of isolation.

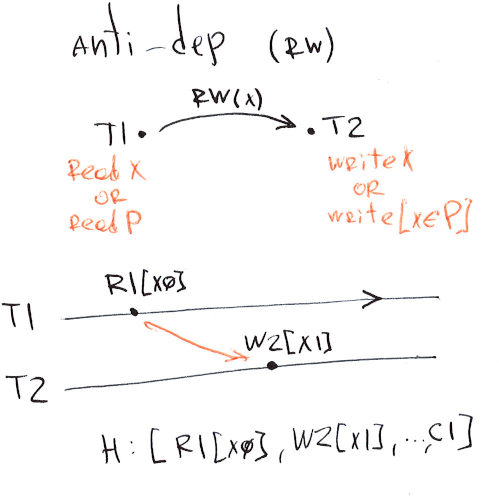
In this example transaction \(T_2\) updates an object \(x\) observed by the transaction \(T_1\) and thus item-anti-depends on \(T_1\). This rw dependency is outlined as an orange arrow in the graph from \(T_1\) to \(T_2\) over \(x\): \(R_1(X_0) -rw[x]-> W_2(X_1)\).

select * from test where id = 1;         -- Ti: Ri(x0)
update test set value = 1 where id = 1;  -- Tj: Wj(x1)

Transaction anomalies

All phenomena are defined in terms of DSG cycles and conflict relations.

G0: dirty writes

G0: Write Cycles. A history H exhibits phenomenon G0 if DSG(H) contains a directed cycle consisting entirely of write-dependency edges.

G0 phenomenon describes what is known as dirty writes because it reflects a case in which updates to \(x\) and \(y\) occurs in opposite order (\(T1:W.x << T2:W.x\), but \(T2:W.y << T1:W.y\)).

The level on which G0 is disallowed called PL-1 or READ UNCOMMITTED.

In this example \(T1\) writes \((x = 2, y = 8)\), and \(T2\) writes \((x = 5, y = 5)\). The outcome of the history H is \((x = 5, y = 8)\) which is inconsistent with any of the executed transaction.

G1: dirty reads

Phenomenon G1 captures the essence of no-dirty-reads, and consists of g1a, g1b, g1c. PL-2 isolation level is defined such that G1 disallowed.

G1a: Aborted Reads (cascaded aborts)

G1a: Aborted Reads. A history H shows phenomenon G1a if it contains an aborted transaction \(T1\) and a committed transaction \(T2\) such that \(T2\) has read some object (maybe via a predicate) modified by \(T\).

G1a is part of the PL-2 isolation level or READ COMMITTED.

It prevents a transaction from committing if it has read the updates of an aborted transaction.

In this example \(T2\) has read an object \(x\) written by aborted transaction \(T1\). Then \(T2\) must be aborted.

G1b: Intermediate Reads (dirty reads)

G1b: Intermediate Reads. A history H shows phenomenon G1b if it contains a committed transaction \(T2\) that has read a version of object \(x\) (maybe via a predicate) written by transaction \(T1\) that was not \(T1\)’s final modification of \(x\).

G1b is part of the PL-2 isolation level or READ COMMITTED.

It ensures that transactions see only final versions of the objects.

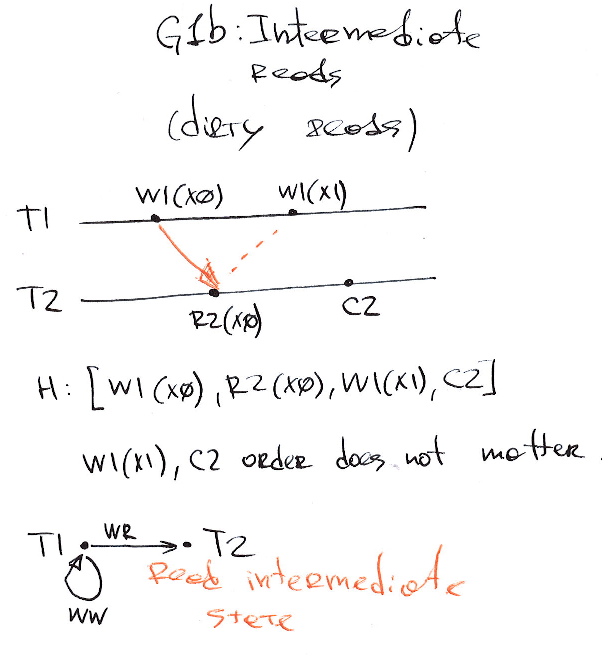
In this example \(T2\) reads an intermediate state (not final) of object \(x_0\) (\(R_2(x_0)\)) written by the \(T1: W_1(x_0)\) and then overwritten with another version \(x_1\). Then \(T2\) must be aborted (can’t be committed).

G1c: Circular Information Flow

G1c: Circular Information Flow. A history H exhibits phenomenon G1c if DSG(H) contains a directed cycle consisting entirely of dependency edges.

G1c is part of the PL-2 isolation level or READ COMMITTED.

It ensures that if transaction \(T2\) is affected by transaction \(T1\), it does not affect \(T1\), i.e., there is a unidirectional flow of information from \(T1\) to \(T2\).

There 3 possible combinations of cycles consisting of \(\{ww, wr\}\) dependencies. g1c does not consider cycles with rw edges.

First example shows ww-ww and wr-ww cycles:

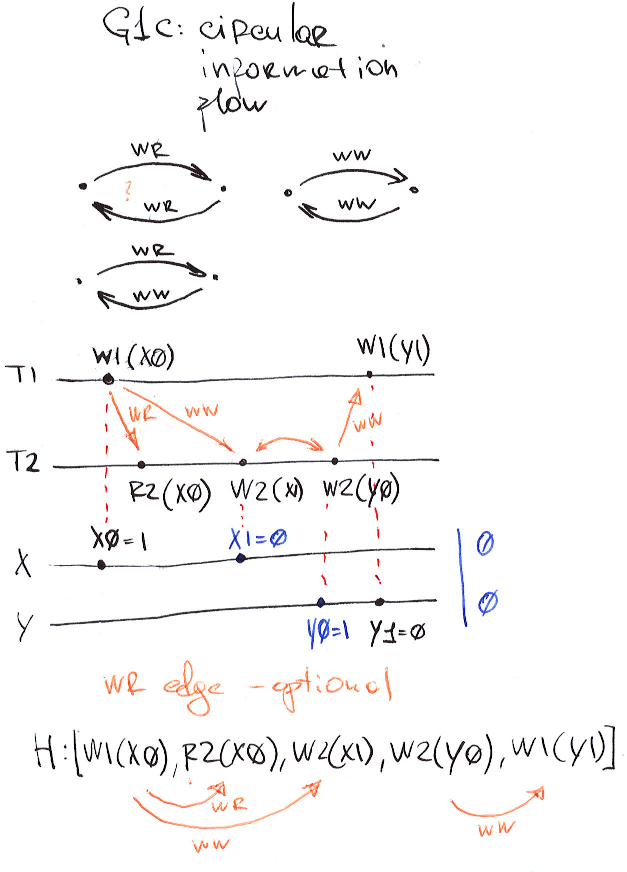
Imagine, a system invariant is defined such that only one button of \(\{x, y\}\) is allowed to be activated simultaneously. Allowed outcomes are \((0,0), (1,0), (0,1)\), but not \((1,1)\).

Now the first transaction \(T1\) will be disabling button \(x\) and activating button \(y\): \((x=0, y=1)\), and the second transaction \(T2\) will do the opposite - it will activate \(x\) and disable \(y\): \((x=1, y=0)\). That is exactly what is needed to create ww-ww cycle: \(W_1(x_0)-ww->W_2(x_1)\), \(W_2(y_0) -ww->W1(y_1)\).

The operator which makes a decision on the second action is allowed to proceed only if the first button was enabled so the \(T2\) reads \(x\) at \(R_2(w_0)\) creating a wr-ww cycle.

\(T1\) and \(T2\) depends on each other. Outcome of history H is \((x=1, y=1)\) - both buttons are activated what breaks system invariant.

Second example shows a wr-wr cycle in which both transactions perform write and read on opposite objects x and y ending up with inconsistent final view:

Initial state of the system is \(\{ x_0=10, y_0=20 \}\). \(T1\) writes \(x_1=11\), and \(T2\) writes \(y_1=22\). Then they read y and x correspondingly and see \(T1: (x=11, y=20)\), \(T2: (x=10, y=22)\), while the actual system state is \(\{ x_1=11, y_1=22 \}\). That means in history H they both observed inconsistent state of the system what must be forbidden for the sake of the greater good.

  T1 ----W(x=11)-R(y=20)-c1----------(x=11,y=20)
  T2 ----W(y=22)-R(x=10)-c2----------(x=22,y=10)
  x  -10-----------------11----------11
  y  -20-----------------22----------12

G-cursor: Lost Update

G-cursor(x) or Single Anti-dependency Cycle over X: A history H exhibits phenomenon G-cursor(x) if LDSG(H) contains a cycle with an anti-dependency (rw) and one or more write-dependency (ww) edges such that all edges are labeled \(x\).

G-cursor describes what is known as lost update.

The level on which G1 and G-cursor are disallowed called PL-CS or Cursor Stability.

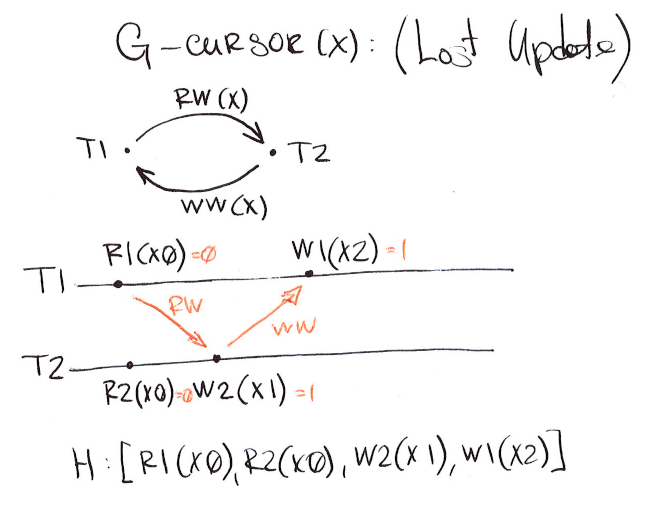
In this example each transaction tries to increment a value \(x\). Each transactions reads \(x\), and then writes updated value back setting \(x=x+1\). It happens to be that \(T1\) and \(T2\) ran concurrently and having rw-ww cycle among each other ends up both setting \(x = 1\) even though they both were incrementing it. \(W_2(x_1)\) update was lost after \(W_1(x_2)\). The right outcome must be \(x = 2\).

G-single: Single Anti-dependency Cycles (read skew)

G-single or Single Anti-dependency Cycle: A history H exhibits phenomenon G-single if DSG(H) contains a cycle consisting of an anti-dependency (rw) and one or more dependency (ww, wr) edges.

G-single describes what is known as a read skew or non-repeatable reads.

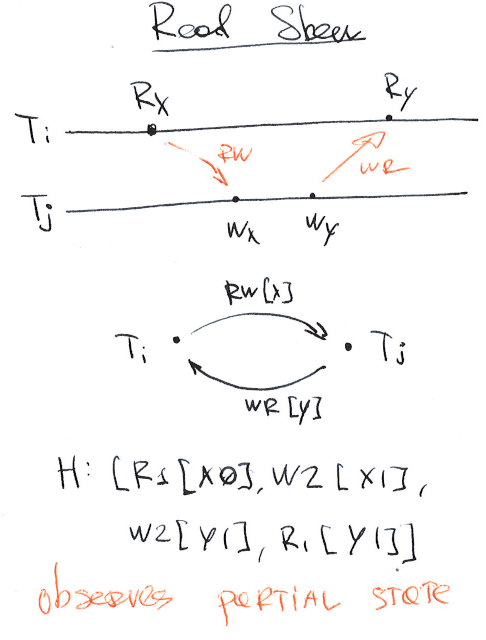
The problem here is that read-only transaction \(T_i\) performing read \((x, y)\) observed \(x\) and \(y\) from various states of the system, thus ended up seeing inconsistent state. \(R_i(x)\) read a version before the committed transaction \(T_j\) wrote a version of \(W_j(y)\) that was then read by \(T_i: R_i(y)\).

  T1 --R(x=0)-----------------R(y=1)--(x=0,y=1) <-- broken
  T2 ---------W(x=1)---W(y=1)---------(x=1,y=1)
  x  --0--------1---------------------1
  y  --0-----------------1------------1

G2-item: Item Anti-dependency Cycles (write skew on disjoint read)

G2-item: Item Anti-dependency Cycles. A history H exhibits phenomenon G2-item if DSG(H) contains a directed cycle having one or more item-anti-dependency (rw) edges.

G2-item describes what is known as a write skew.

The level on which G2-item is disallowed called PL-2.99 or REPEATABLE READ.

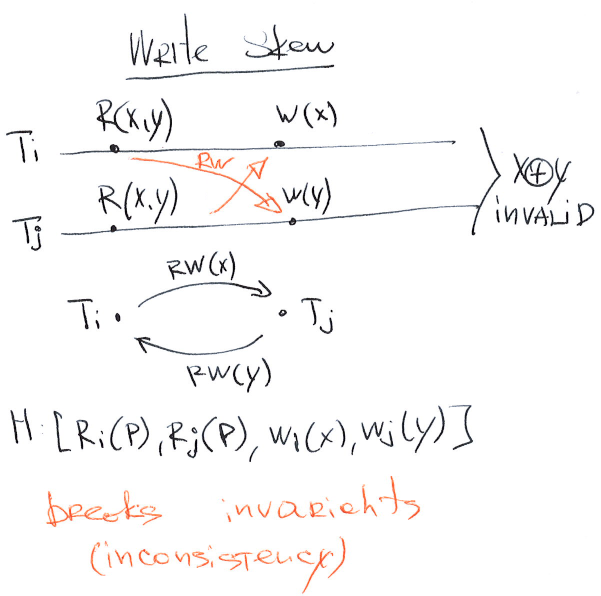
In this example we have an invariant that only one of the objects may be activated \(x + y <= 1, \{x, y\} = \{0, 1\}\). A transaction first reads both objects \((x, y)\) and tries to activate one of them. So the \(T_i\) reads \((x=0, y=0)\) and writes \((x = 1)\), and the \(T_j\) reads \((x=0, y=0)\) and writes \((y = 1)\). In the end both commits and end up with broken invariant \((x = 1, y = 1), x + y > 1\).

This happens due to the presence of rw edges in the DSG(H): \(R_i(y) -rw-> W_j(y)\), \(R_j(x) -rw-> W_j(x)\).

  T1 --R(x=0,y=0)-------W(x=1)--------(x=1,y=0)
  T2 --R(x=0,y=0)-------W(y=1)--------(x=0,y=1)
  x  --0-----------------1------------1         | both
  y  --0-----------------1------------1         | are 1

G2: Anti-Dependency Cycles (write skew on predicate read)

G2: Anti-dependency Cycles. A history H exhibits phenomenon G2 if DSG(H) contains a directed cycle with one or more anti-dependency (rw) edges.

G2 describes what is known as a write skew. G2 differ from the G2-item by including predicates.

The level on which G2 is disallowed called PL-3 or SERIALIZABLE.

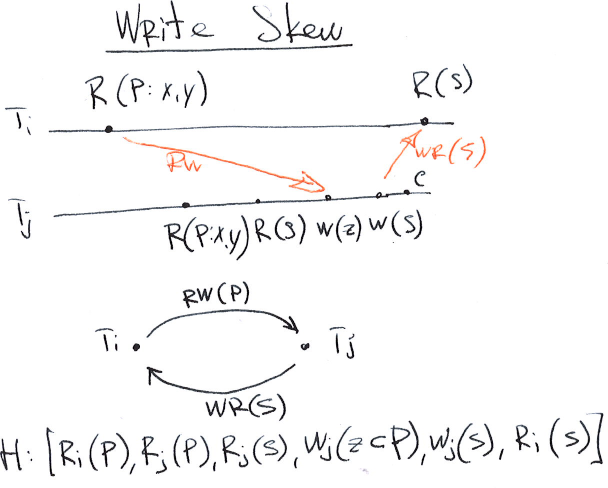
Here we have a read-only transaction which observes reads from various states of the system. It reads \((x, y)\) using predicate \(P\), and then reads its sum \(S\) which must be \(S = x + y\).

Concurrently the second transaction writes new object \(z\) that changes matches of predicate \(P\) and updates an object \(S\) to be \(S = x + y + z\). Then the first transaction reads \(S = x + y + z\) and ends up with invalid state observing: \((\{x, y\}, S = x + y + z)\).

  T1 --R(P:x=1,y=1)-------------------R(S=3)-(x,y=1,z=3) <--
  T2 --R(P:x,y)-----W(z=1)-W(S=x+y+z)--------(x,y,z=1,s=3)
  x  --1-------------------------------------1
  y  --1-------------------------------------1
  z                 --1----------------------1
  s  --2---------------------3---------------3

OTV: Observed Transaction Vanishes

Observed Transaction Vanishes (OTV). A history H exhibits phenomenon OTV if USG(H) contains a directed cycle consisting of exactly one read-dependency (wr) edge by \(x\) from \(T_j\) to \(T_i\) and a set of edges by \(y\) containing at least one anti-dependency (rw) edge from \(T_i\) to \(T_j\) and \(T_j\)’s read from \(y\) precedes its read from \(x\).

OTV occurs when a transaction observes part of another transaction’s updates but not all of them and then observed partial state completely vanishes (gets out of existence).

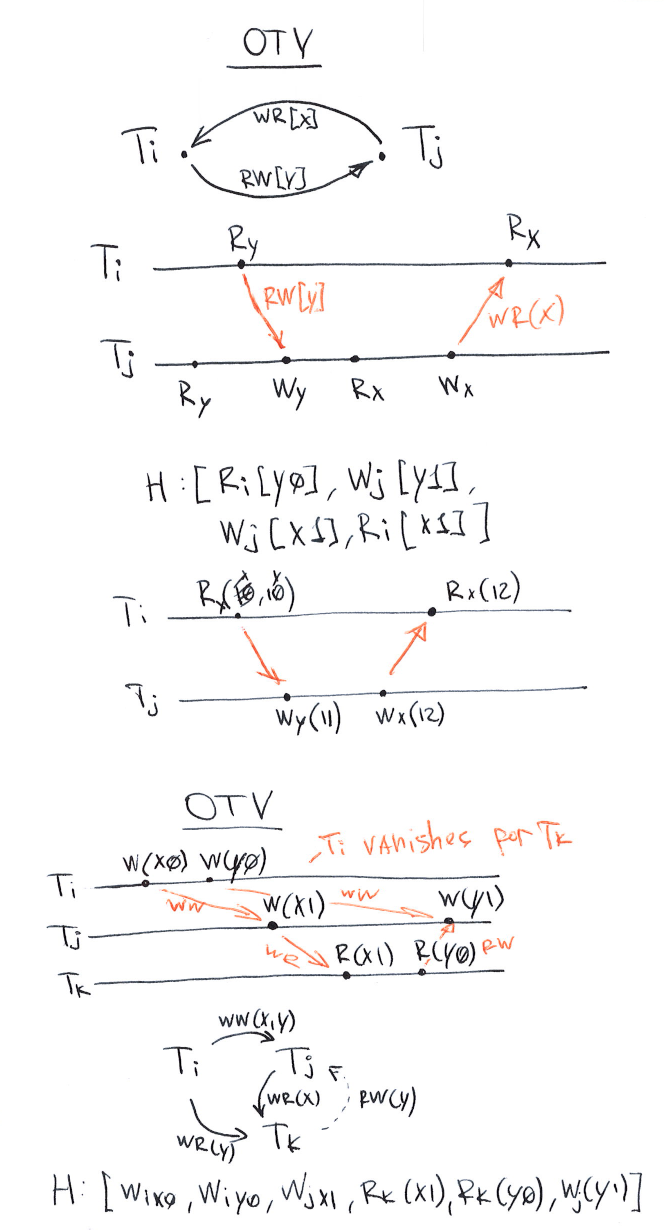
Speaking of the second example we have 3 transactions \(T_i, T_j, T_k\). \(T_k\) (not necessarily a read-only transaction) observes partially \(T_i\) updates reading \(R_k(y_0)\) which then vanishes being overwritten by the \(T_j: W_j(y_1)\) even before the \(T_k\) finishes (commits).

Thus, \(T_k\) has observed partial state \(y_0\) of \(T_i\) which then vanished (\(T_j\) commits before \(T_k\) and sets \(W_j(y_1)\)).

  T1 --W(x=1)---W(y=1)----c1-----------------(x=1,y=1)
  T2 --------W(x=2)-------------W(y=2)-c2----(x=2,y=2)
  T3 --------------R(x=2)-R(y=1)-------------(x=2,y=1)
  x  --1-------2-----------------------------2      ^
  y  -------------1---------------2----------2      \- y=1 not exists

SQL [hermitage/postgres/otv]:

PostgreSQL “read committed” prevents Observed Transaction Vanishes (OTV):

create table test (id int primary key, value int);
insert into test (id, value) values (1, 0), (2, 0);
begin; set transaction isolation level read committed; -- T1
begin; set transaction isolation level read committed; -- T2
begin; set transaction isolation level read committed; -- T3
update test set value = 1 where id = 1;  -- T1: W1(x=1)
update test set value = 1 where id = 2;  -- T1: W1(y=1)
update test set value = 2 where id = 1;  -- T2: W2(x=2) BLOCKS
commit; -- T1. This unblocks T2
select * from test where id = 1;         -- T3: R3(x=2)
update test set value = 2 where id = 2;  -- T2: W2(y=2)
select * from test where id = 2;         -- T3: R3(y=1)
commit; -- T2
select * from test where id = 2;         -- T3: R3(y=2)
select * from test where id = 1;         -- T3: R3(x=2)
commit; -- T3

IMP/PMP: Predicate-Many-Preceders

Item-Many-Preceders (IMP). A history H exhibits phenomenon IMP if DSG(H) contains a transaction \(T_i\) such that \(T_i\) directly item-read-depends (wr) by \(x\) on more than one other transaction.

IMP occurs if a transaction observes multiple versions of the same item (e.g., transaction Ti reads x1 and x2).

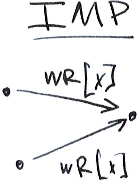
  T1 --W(x=1)--------------------------------(x=1)
  T2 -----------W(x=2)-----------------------(x=2)
  T3 -----------------R(x=2)-R(x=1)----------(x={1,2})
  x  --1?---------2?-------------------------?

Predicate-Many-Preceders (PMP). A history H exhibits the phenomenon PMP if, for all predicate-based reads \(r_i(P_i : Vset(P_i))\) and \(r_j(P_j : Vset(P_j)\) in \(T_k\) such that the logical ranges of \(P_i\) and \(P_j\) overlap (call it \(P_o\)), the set of transactions that change the matches of \(P_o\) for \(r_i\) and \(r_j\) differ.

PMP occurs if a transaction observes different versions resulting from the same predicate read (e.g., transaction \(T_i\) reads \(Vset(P_i) = ∅\) and \(Vset(P_i) = {x_1}\))).

Both IMP and PMP relates to the Snapshot isolation mode (Snapshot Isolation prevents G0, G1a, G1b, G1c, PMP, OTV, and Lost Updates phenomena).

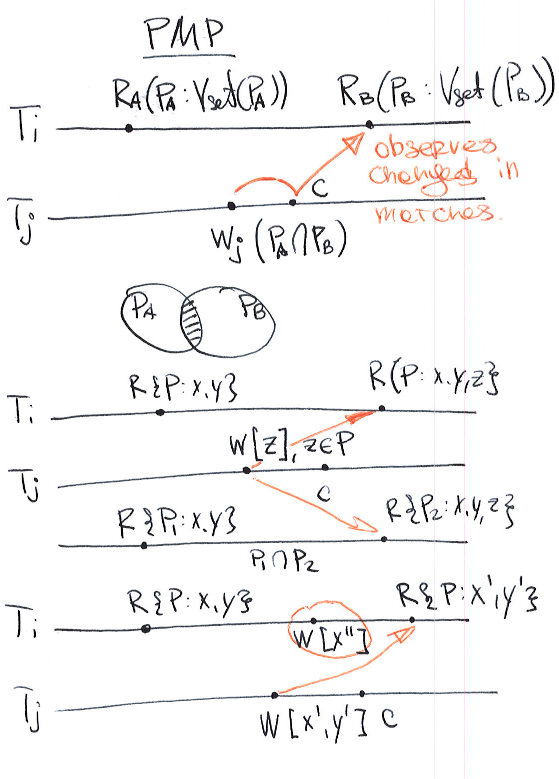
First example

\(T_i\) performs 2 consecutive predicate-reads such that \(P_0 = P_a \cap P_b\). \(T_j\) changes matches of \(P_0\) writing new object \(z\).

  T1 --R(Pa:x=10,y=10)----R(Pb:x,y=10,z=20)--(x,y=10,z=20)
  T2 ---------------W(z=20)------------------(z=20)
  x  --10------------------------------------10
  y  --10------------------------------------10
  z                 --20---------------------15

  Pa: n > 0
  Pb: n mod 5 == 0
  P0: n > 0 and n mod 5 == 0

SQL [hermitage/postgres/pmp]:

PostgreSQL “read committed” does not prevent Predicate-Many-Preceders (PMP):

create table test (id int primary key, value int);
begin; set transaction isolation level read committed; -- T1
begin; set transaction isolation level read committed; -- T2
select * from test where value > 0;          -- T1. Returns nothing
insert into test (id, value) values (1, 5);  -- T2
commit; -- T2
select * from test where value % 5 = 0;      -- T1. Returns the inserted row
commit; -- T1

Second example

\(T_i\) performs 2 consecutive predicate reads such that \(P_0 = P_a \cap P_b\). In between of these reads it install new version of object \(x\) (update/delete) which gets completely lost behind versions written by just committed \(T_j\).

  T1 --R(Pa:x=10,y=10)-W(x=11)-R(Pb:x,y=20)--(x,y=10,z=20)
                          | blocks until c2
                          \---------\
                                    v
  T2 ---------------W(x=20)-W(y=20)-c2-------(x=20)
  x  --10-------------20----------------------20
  y  --10---------------------20--------------20

  Pa: n > 0
  Pb: n mod 5 == 0
  P0: n > 0 and n mod 5 == 0

Here \(W_1(x = 11)\) completely vanishes. This op could be delete.

SQL [hermitage/postgres/pmp]:

PostgreRQL “read committed” does not prevent Predicate-Many-Preceders (PMP) for write predicates:

create table test (id int primary key, value int);
insert into test (id, value) values (1, 10), (2, 20);
insert into test (id, value) values (1, 10), (2, 20);
begin; set transaction isolation level read committed; -- T1
begin; set transaction isolation level read committed; -- T2
update test set value = value + 10;  -- T1
delete from test where value = 20;   -- T2, BLOCKS
commit; -- T1. This unblocks T2
select * from test where value = 20; -- T2, returns 1 => 20 (despite ostensibly having been deleted)
commit; -- T2

Short-fork/ Long-fork (write-skew)

Short-fork and Long-fork phenomena are given in the context of Parallel Snapshot Isolation (PSI) described in [9] and [11].

Advantage of the PSI transactional model (to SI) is the ability of achieving total availability at the costs of having long-forks [10].

Citing the [9]:

Short fork happens when transactions make concurrent disjoint updates causing the state to fork. After committing, the state is merged back.

     /(0,0)--T1:(1,0)--\
    /                  v
---o(0,0)--------------x(1,1)---
    \                  ^
     \(0,0)--T2:(0,1)--/

or in other words:

  T1 --R(x=0,y=0)-------W(x=1)----c1--(x=1,y=0)
  T2 --R(x=0,y=0)-------W(y=1)----c2--(x=0,y=1)
  x  --0-----------------1------------1         | both
  y  --0-----------------1------------1         | are 1

This is exactly what is classical G2-item or write-skew.

Long fork happens when transactions make concurrent disjoint updates causing the state to fork. After they commit, the state may remain forked but it is later merged back.

     /(0,0)--T1:(1,0)-T2:(1,0)--\
    /                           v
---o(0,0)-----------------------x(1,1)---
    \                           ^
     \(0,0)--T3:(0,1)-T4:(0,1)--/

it could be:

                      T2:(x=1,y=0,a=x+1)-\
                      /                   \
     /(x=0,y=0)--T1:(x=1,y=0)-------------x
    /                                     v
---(x=0,y=0)----------------------(x=1,y=1,a=2,b=3)---
    \                                     ^
     \(x=0,y=0)--T3:(x=0,y=1)-------------x
                      \                   /
                      T4:(x=1,y=0,b=y+2)-/

It is almost classical write-skew with the ability to have transactions executed over a forked state branches, yet it is still a write-skew.

Citations

All definitions are taken from [1], [2], [3].

Big thanks to Adrian Colyer for his review of [1] in the morning paper.

References

Related Posts

blog comments powered by Disqus