Testing serializability classes
18 Apr 2020Recently, I came across an excellent exercise of testing a scheduling history for belonging to different serializability classes and had a lot of fun drawing a polygraph and finding out a cycle in it. When I finally managed to draw the correct version of the polygraph, I thought that it could be interesting to someone wondering to learn how testing for view state serializability looks like.
I was fascinated by how scary the result looks like and wanted to share my excitement.
In this article, I will show how to find out to what serializability class the following history
\[s = r_1(x) r_3(x) w_3(y) w_2(x) r_4(y) c_2 w_4(x) c_4 r_5(x) c_3 w_5(z) c_5 w_1(z) c_1\]belongs. Basically we will be looking at final state serializability (FSR), view state serializability (VSR) and conflict state serializability (CSR).
First of all, let’s take a look at steps grouped by transaction id:
Here, we have 5 transactions \(t_1, t_2, t_3, t_4, t_5\). We imply complete history with \(t_0, t_{inf}\), where \(op_i(x)\) means read or write operation in transaction \(i\) of a data item \(x\).
Let’s start with a testing for the CSR. To do that, we will draw the conflict graph \(G(s)\).
For the greater fun let’s start with a drawing of the conflict step graph \(D_2(s) = < V = op(s), E = {conf}(s) >\).
Note. \(conf(s) := \{(p, q)\ |\ p, q\ \text{are in conflict in}\ s\ \text{and} \ p\ <_s\ q \}\) is called the conflict relation of \(s\).
Note. Two data operations \(p \in t\) and \(q \in t'\) (t != t’) are in conflict in \(s\) if they access the same data item and at least one of them is a write.
The cycle is easy to see here at:
\[\{(r_1(x), w_2(x)), (w_2(x), r_5(x)), (w_5(z), w_1(z))\} \subset conf(s)\]However, let’s show that the conflict graph \(G(s)\) is not acyclic and thus \(s \notin {CSR}\):
We have proved that \(s\) does not belong to the CSR class. It is time to test if \(s\) belongs to the VSR - the most funniest part of the exercise. We first test if \(s \in VSR\) and then if it does find \(s' - serial | s \approx_v s'\).
To verify if \(s \in VSR\) we must prove that the polygraph of \(s\) is acyclic. That means that there exists a compatible graph \(G(s)\) that is acyclic.
To make understanding simpler let’s take a look at useful steps in \(s\) first.
Note. A step \(p\) is directly useful for a step \(q\), denoted \(p \rightarrow q\), if \(q\) reads from \(p\), or if \(p\) is a read step and \(q\) a subsequent write step from the same transaction.
Note. \(RF(s)\) is a read-from relation over \(s\) defined as \(RF(s) = {(t_i, x, t_j)\ |\ \text{an}\ r_j(x)\ \text{reads}\ x\ \text{from a}\ w_i(x)}\).
Blue lines depict \(RF(s)\) relation. In example in pair \((r_1(z), e_1) \in RF(s), e_i = t_\infty\) the transaction \(t_\infty\) reads \(z\) from the latest write in \(s\) of \(z\) from transaction \(t_1\) as defined by the \(H[s]\) (\(H[s](z) = H_s(w_1(z))\)).
Let’s also add a few important conflicts from the \(conf(s)\) to our graph to see where we are having cycle in choices.
Those conflicts clearly demonstrate the limits until which the transactions can be moved before breaking their \(RF(s)\) relation with \(s' - serial\). Having those conflicts depicted it can be clearly seen that there is no such a serial transaction exist that \(s'\ -\ \text{serial}\ |\ s \approx_v s'\) due to the cycle in relation with \(t_1\):
\[t_1 <_{s,x}\ t_2 <_{s,x}\ t_4 <_{s,x}\ t_5 <_{s,z}\ t_1\]Simply saying \(t_1\) must be before \({t_2, t_4, t_5}\) and after at the same time in imaginary serial schedule.
Now, having all that in mind, let’s draw a polygraph \(P(s) = <V\ =\ {trans}(s) \bigcup \{ t_0, t_\infty \}, E\ =\ RF(s) \bigcup (t_0, t) \bigcup (t, t_\infty) \bigcup C | t \in {trans}(s) >\) and prove we were right.
We will start with drawing only \((V, E)\) part of the \(P(s)\) without choices (C) for simplicity.
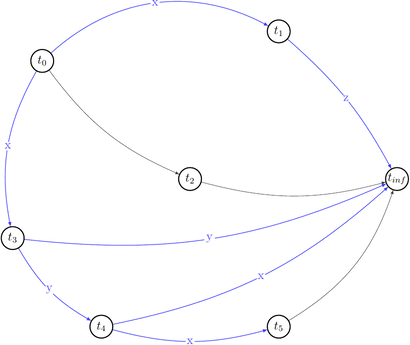
Ok, it looks simple. No cycles yet. Let’s draw choices set of \(P(s)\) that is: \(C\ =\ \{(t',\ t′′,\ t)\ |\ (t,\ t′)\ \in\ E\ \land\ t′\ \text{reads}\ x\ \text{from}\ t\ \land\ \text{some}\ w(x)\ \text{from}\ t′′\ \text{appears somewhere in}\ s \}\). Besides that they are alternative variants of dependencies. They depict existing conflicts.
How a choice looks like: for example for \((t_0, x, t_1) \in RF(s) \equiv (t_0, t_1) \in E\) the choice is \((t_1, t_2, t_0) \in C(s)\) because \(\exists\ w_2(x) \in t_2\ |\ t_1\ \text{reads}\ x\ \text{from}\ t_0: w_0(x) \rightarrow r_1(x)\) and we draw 2 possible edges \((t_1, t_2), (t_2, t_0)\).
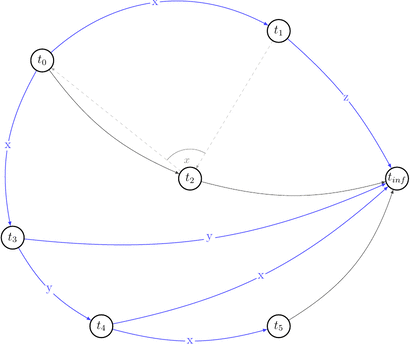
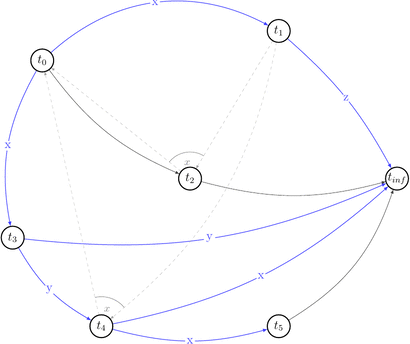
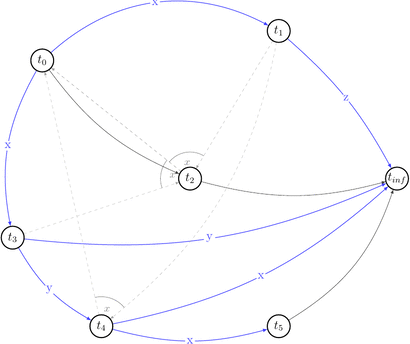
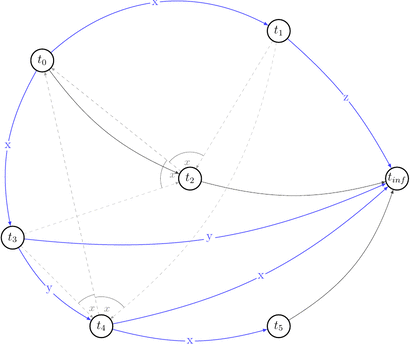
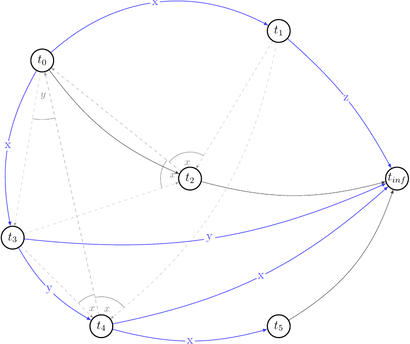
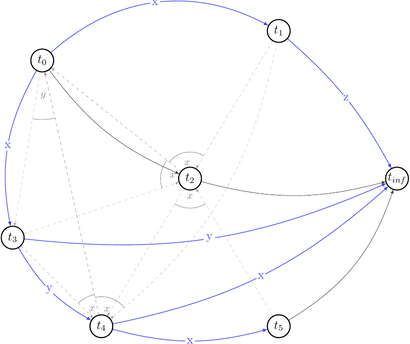
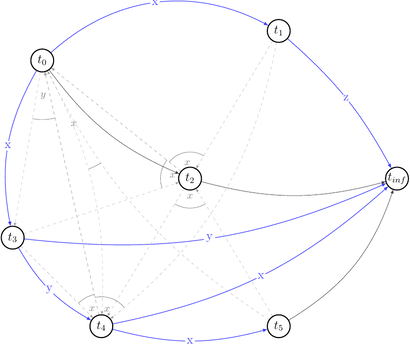
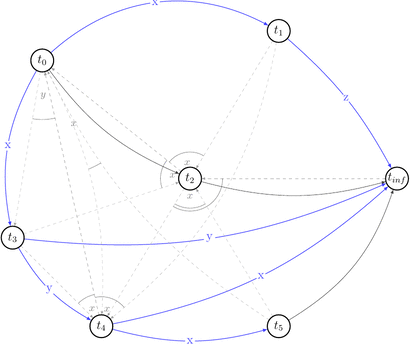
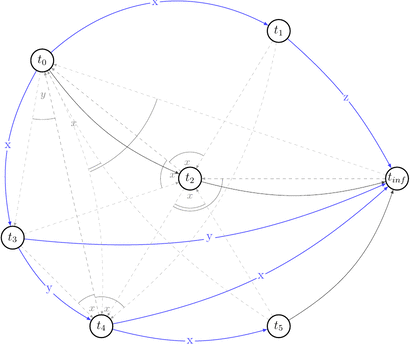
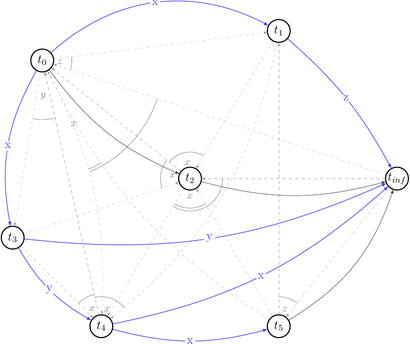
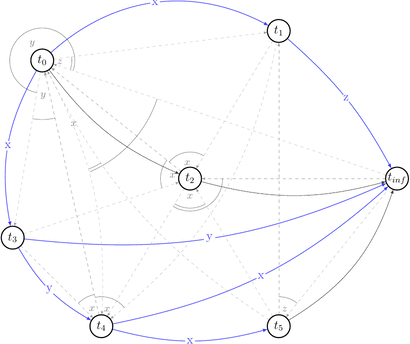
Let’s reduce number of uninteresting choices by picking choices that do not lead to the cycles in \(P(s)\). Thus we will draw partially compatible graph \(G(s)\) to the polygraph along the way.
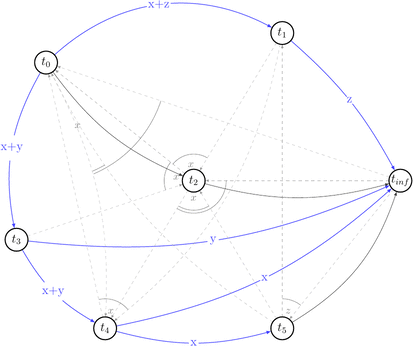
Few choices were reduced by the existing edges.
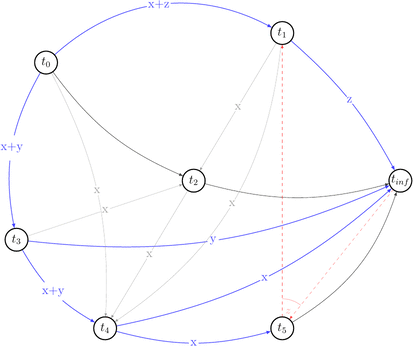
Red dashed arrows depict choices that can’t be reduced without introducing a cycle into a compatible graph. Thus, we can’t build a compatible graph for the polygraph \(P(s)\) such that this graph will have no cycles. Hence, \(P(s)\) is not acycle and \(s \notin {VSR}\).
Now, it’s time to prove that \(s \in {FSR}\). FSR is a finite state serializability and as it follows from the it’s name we are only interested in final states. We will be not looking at intermediate inconsistencies in \(RF(s)\).
Note. \(s \in {FSR}\ \text{if}\ \exists\ s'\ \text{- serial}\ | \ op(s) = op(s')\ \land\ LRF(s) = LRF(s')\)
\[LRF(s) = \{ (t_1, z, t_\infty), (t_4, x, t_\infty), (t_3, y, t_\infty), (t_3, y, t_4), (t_0, x, t_3), (t_0, x, t_1) \}\]Let’s take a look at a serial history:
\[s'\ =\ t_5 t_1 t_3 t_2 t_4\] \[LRF(s') = \{ (t_1, z, t_\infty), (t_4, x, t_\infty), (t_3, y, t_\infty), (t_3, y, t_4), (t_0, x, t_3), (t_0, x, t_1) \}\]Since \(LRF(s) = LRF(s')\) it follows that \(s \in FSR\).
That’s basically it.
Have fun.